本文へスキップ

ロゴ２

硬さ標準片

硬さ標準片って何？

硬さ試験は、材料の引張り強さの代用特性を求めるために、工業的に考えられた試験方法であり、機械部品の強度や熱処理などの品質評価等に広く行われています。 しかし、硬さ試験機は試験機によって色々な硬さ値を指示することが多いので、製品の品質の信頼性を確保するためには、標準を用いて試験機を校正することが極めて重要であります。
ところが、硬さは工業的な約束によって成立する工業量であるので、硬さ値については古くから色々な考えかたがあって、国際的にも国内的にもいくつもの基準が存在する状態が長い間続きました。
計量研究所は、硬さ試験方法に表現された約束事をできるだけ忠実に実現しようという考え方で硬さ標準の研究を行い、1960〜1965年の間に各種硬さの標準値を設定しました。
硬さ標準片は、写真に示されるように硬さ標準値を表示してある標準物質の１つとして、硬さ試験機の校正や管理に使用されるものであります。ＪＩＳ規格では硬さ基準片と呼んでいますが、従来から慣用的に用いられた硬さ基準と区別する意味で、計量研究所が設定した国の硬さ標準値が値付けられているものを特に計量研究所では硬さ標準片と呼んでいます。

当社では品質工学の手法を用いて、高精度の各種硬さ標準片を開発し、販売しております。

硬さ標準値の精度とはどういうもの？

硬さ標準片標準の考え方には、要素統合型と比較統合型とがあります。要素統合型の標準は、標準を規定するいくつかの要素を定め、それを装置として合成すれば正しい値が得られるという考え方であり、比較統合型の標準は唯一の拠り所となる標準が得られない場合、各事業所で測定された測定値の平均を求めるという考え方です。この両者は相互補完的であり、いずれか一方だけで正しいとは言いがたいのですが、現実には補完させることが困難な場合が多いのです。 硬さ標準の場合は、要素統合型の考え方を基本として、比較統合型との補完を行って設定されました。
硬さ標準の中から、ロックウェル硬さ標準について詳しく述べます。
ロックウェル硬さ標準は、ロックウェル硬さの定義として明示されている部分を試験機、圧子に実現し、かつオリジナルの考えにできるだけ沿って、計測的に設定されるべきものであるとの考え方で設定されました。Ｗｉｌｓｏｎ社のオリジナルな試験機は槓杆型であり、標準試験機も槓杆型を採用して、要素統合型で、設計し、試験機の各構成要素の誤差要因の効果を総合的に評価した後に、ロックウェル硬さの定義に明示されている部分を可能な限り忠実に標準試験機に実現しました。 圧子についても、同様な考え方のもとに定義として明示されている形状に比較的近い良好な数十本の圧子を標準圧子群として、その形状を精度の高い方法によって計測し、これらの標準圧子群によって測定された硬さ値との関係を、形状誤差をパラメータとした重回帰式の不偏推定値として定義通りの圧子の形状を持った圧子によって得られる硬さ値を推定しました。 したがって、個々の標準圧子は、この不偏推定値によって校正された補正値が与えられます。
　この様にして設定されたロックウェル硬さ標準値の誤差は、ＨＲＣ６０について表わすと、表１の通りになります。

要　素 回帰係数β（ＨＲＣ／ｇ） 誤差の大きさ（ＨＲＣ）
１．基準荷重の誤差（±４．６ｇ） ２．８×１０-4 ±０．００
２．試験荷重の誤差（±１０．８ｇ） −１．８×１０-4 ±０．００
３．指示系の誤差（±０．２μｍ）   ±０．１０
４．１次標準圧子の形状校正誤差   ±０．１２
５．偶然誤差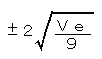式 Ｖｅ０．０１ ±０．０７
６．標準の誤差   ±０．１７
表１

　回帰係数は、荷重が１ｇ異なった場合に変化する硬さ値の割合を示すもので、１の基準荷重の場合は、標準試験機の基準荷重の許容差が±４．６ｇであるので、基準荷重が定義で定められた荷重と４．６ｇ異なった場合に変化する硬さ値の大きさは、４．６×２．８×１０-4＝０．００１２９ＨＲＣ≒０．００ＨＲＣとなります。
　同様にして２の試験荷重の場合も、１０．８×（−１．８×１０-4）＝０．００１９４≒０．００ＨＲＣとなります。
　３の指示系の誤差は、指示系の許容差が±０．２μｍであり、１ＨＲＣの硬さ値を押込み量に換算すると２μｍに相当しますので、硬さ値の誤差は±０．１０ＨＲＣとなります。
　４の１次標準圧子の形状校正誤差は、形状誤差をパラメータとした重回帰式の不偏推定値によって校正された後の校正し切れない硬さ値の誤差で、±０．１２ＨＲＣとなります。
　５の偶然誤差は、１〜４の要素に含まれない標準試験機の経時的な変動や標準片のばらつきなどが含まれている偶然的な誤差で、誤差分散Ｖｅ＝０．０１でｎ＝９の場合±０．０７ＨＲＣとなります。
　したがって、総合的な標準の誤差は、１〜５の２乗和をとって、

となります。

そして、設定された硬さ標準を標準試験機で新たな標準片に値づけするときの供給の誤差は、表２の通りになります。

要　素 誤差の大きさ（ｎ＝９）
６．標準の誤差 ±０．１７
７．２次標準圧子の形状校正誤差 ±０．２５
８．標準のばらつき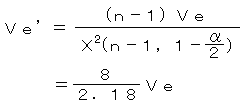式 Ｖｅ’＝０．０４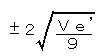式

　　　＝±０．１３
９．標準供給の誤差 ±０．３３
表２

　標準片の値づけは、４の１次標準圧子によって校正された２次標準圧子を用いて行うことから、７の２次標準圧子の形状校正誤差は、±０．２５ＨＲＣとしています。
　８の標準片のばらつきは、表１の５偶然誤差は使用面を代表する９点を測定したときのばらつきであり、９点の測定値から使用面全体のばらつきを推定する必要があるので、これをＪＩＳＺ９０５８（母分散の区間推定）によって推定したＶｅ’を用いています。 したがって、標準供給の誤差は６〜８の２乗和をとって、

となり、これを標準値の精度として、０．０５ＨＲＣ単位に丸めて±０．３５ＨＲＣと表示しています。
　従来から、硬さ標準片の品質の評価の尺度として、ばらつきＲ（測定値の最大値−測定値の最小値）が用いられています。 そして、標準値の精度がばらつきＲと同じように見られることも多いように思われます。 しかし、表２で明らかのように、ばらつきＲは、表２の８に相当するもので、標準値の精度の一部分でしかありません。 表２の８のＶｅ’をばらつきＲに変換すると、ＪＩＳＺ８４０２（分析・試験の許容差通則）から、

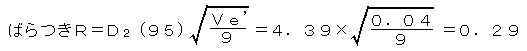
ただし、Ｄ２（９５）＝４．３９（ｎ＝９の場合）
となります。
　ばらつきＲの小さな硬さ標準片を希望されることがありますが、硬さ標準片の品質はばらつきＲの大きさだけでは決まりません。 硬さ標準片として重要なことは、硬さ標準値が変動しないということです。 異なる標準試験機や標準圧子を使用して値づけしても、値づけする日時が違っても、標準値が変動しないことが大切です。 しかし、標準試験機にも若干の変動があり、標準圧子にも圧子間に校正し切れない誤差が存在することや、その上に標準片にもばらつきがあることから、常に同一の標準値が得ることは極めて困難です。 例えば、硬さ標準値がＨＲＣ６０．１０と値づけされた硬さ標準片が後日に再測定したとき標準値がＨＲＣ６０．３０と値づけされたとき、どちらが正しいかという話になります。 しかし、どちらが正しいかということは適切ではなく、どちらも正しいという言い方もできます。 結局、標準値は精度の範囲内で保証されているということです。標準値が変動する可能性の目安として、標準値の精度という形で表しています。 他の硬さ標準値の精度も、同様な考え方で決められています。

表３に代表的な硬さの標準値の精度（信頼率９５％）を示します。

硬さの種類 標準値の精度
ＨＲＣ（ｎ＝９） ４０以上 ±０．３５ＨＲＣ
４０未満 ±０．４０ＨＲＣ
ＨＲ３０Ｎ（ｎ＝９） ７０以上 ±０．５０ＨＲ３０Ｎ
７０未満 ±０．５５ＨＲ３０Ｎ
ＨＶ３０（ｎ＝９） ５００以上 ±０．５％
５００未満 ±０．４％
ＨＶ０．２（ｎ＝９） ８００以上 ±４．０％
５００以上 ±３．５％
５００未満 ±３．０％
ＨＢ（ｎ＝３） ４００以上 ±１．０％
３００以上 ±１．１％
３００未満 ±１．３％
ＨＳ（ｎ＝９） ９７以上 ±１．０ＨＳ
７０以上 ±０．８ＨＳ
６０以上 ±０．７ＨＳ
４０以上 ±０．６ＨＳ
３０以上 ±０．５ＨＳ
３０未満 ±０．４ＨＳ
表３

旭グループ

〒678-0091
兵庫県相生市矢野町菅谷214番地の1

(株)旭工業所
TEL 0791-29-0211
FAX 0791-29-1132

(株)アサヒ技研
TEL 0791-29-1213
FAX 0791-29-1132